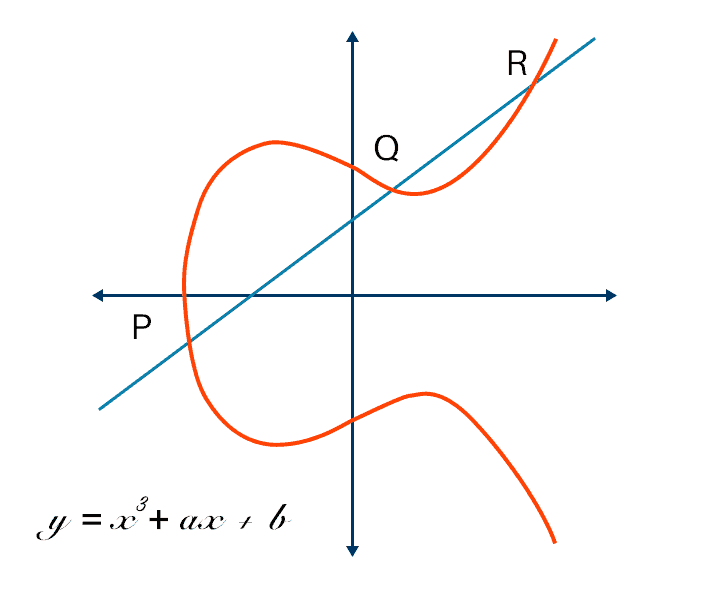Elliptic Curve point addition error when using mixed Jacobian-affine coordinates (CVE-2024-26317)
Description: hey folks welcome to new blog post you have already read the title, if you don’t know i personally love mathematics and Cryptography so this is the post about it about how Elliptic Curve point addition error when using mixed Jacobian-affine coordinates
Target: illumos-gate OS
Issue: Issue with elliptic curve addition in mixed Jacobian-affine coordinates
Elliptic Curve Elliptic curve cryptography (ECC) is a type of public-key cryptography based on the algebraic structure of elliptic curves over finite fields. It utilizes the mathematical properties of elliptic curves to perform cryptographic operations like key exchange, digital signatures, and encryption.
An elliptic curve is a mathematical structure defined by an equation of the form:
y^2 = x^3 + ax + b
This equation defines a curve that satisfies specific properties. The elliptic curve equation involves two parameters, (a) and (b), which determine the curve’s shape. These parameters, along with a finite field modulus (p) (which defines the field over which the curve operates), uniquely define the elliptic curve.
The elliptic curve equation forms a set of points ((x, y)) that satisfy the equation. However, in cryptographic applications, the curve is defined over a finite field (F_p), where (p) is a prime number, and the points on the curve represent solutions within this finite field.
The properties of elliptic curves, such as their smoothness, symmetry, and group structure, are utilized in ECC to enable secure cryptographic operations. ECC offers several advantages over other cryptographic systems, including smaller key sizes for equivalent security levels compared to RSA and Diffie-Hellman algorithms.
Elliptic Curve Implementation in C
Heres a simple example of elliptic curve operations in C using OpenSSL. This example demonstrates key generation and signature creation using the secp256k1 curve, which is commonly used in Bitcoin
This C program uses OpenSSL for elliptic curve operations. It generates a key pair, prints the private and public keys in hexadecimal format, signs a message, prints the signature, and verifies the signature. Make sure you have OpenSSL installed on your system, and when compiling, link against the OpenSSL library using -lssl -lcrypto.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <openssl/ec.h>
#include <openssl/obj_mac.h>
#include <openssl/ecdsa.h>
#include <openssl/rand.h>
void handleErrors() {
fprintf(stderr, "An error occurred\n");
exit(EXIT_FAILURE);
}
EC_KEY* generateKeyPair() {
EC_KEY *ec_key = EC_KEY_new_by_curve_name(NID_secp256k1);
if (!ec_key) handleErrors();
if (!EC_KEY_generate_key(ec_key)) handleErrors();
return ec_key;
}
void printHex(const char *label, const unsigned char *data, size_t len) {
printf("%s: ", label);
for (size_t i = 0; i < len; i++) {
printf("%02X", data[i]);
}
printf("\n");
}
void signAndVerifyExample() {
EC_KEY *ec_key = generateKeyPair();
// Get private and public keys
const BIGNUM *private_key = EC_KEY_get0_private_key(ec_key);
const EC_POINT *public_key = EC_KEY_get0_public_key(ec_key);
// Convert keys to binary
size_t private_key_size = BN_num_bytes(private_key);
size_t public_key_size = EC_POINT_point2oct(
EC_KEY_get0_group(ec_key),
public_key,
POINT_CONVERSION_UNCOMPRESSED,
NULL,
0,
NULL
);
unsigned char *private_key_bin = malloc(private_key_size);
unsigned char *public_key_bin = malloc(public_key_size);
BN_bn2bin(private_key, private_key_bin);
EC_POINT_point2oct(
EC_KEY_get0_group(ec_key),
public_key,
POINT_CONVERSION_UNCOMPRESSED,
public_key_bin,
public_key_size,
NULL
);
// Print keys
printHex("Private Key", private_key_bin, private_key_size);
printHex("Public Key", public_key_bin, public_key_size);
// Sign a message
const char *message = "Hello, Elliptic Curve!";
size_t message_len = strlen(message);
unsigned char *signature = malloc(ECDSA_size(ec_key));
unsigned int signature_len;
if (!ECDSA_sign(
0,
(const unsigned char *)message,
message_len,
signature,
&signature_len,
ec_key
)) {
handleErrors();
}
// Print signature
printHex("Signature", signature, signature_len);
// Verify the signature
if (ECDSA_verify(
0,
(const unsigned char *)message,
message_len,
signature,
signature_len,
ec_key
) != 1) {
fprintf(stderr, "Signature verification failed\n");
} else {
printf("Signature verified successfully\n");
}
// Clean up
free(private_key_bin);
free(public_key_bin);
free(signature);
EC_KEY_free(ec_key);
}
int main() {
// Seed the random number generator
if (RAND_poll() != 1) {
fprintf(stderr, "RAND_poll() error\n");
return EXIT_FAILURE;
}
// Initialize OpenSSL
OpenSSL_add_all_algorithms();
// Run the example
signAndVerifyExample();
// Clean up OpenSSL
EVP_cleanup();
return EXIT_SUCCESS;
}
this code tested on ubuntu 22.04 LTS but will work all the distros, to run it you you’ll need to have OpenSSL installed. If you don’t have it installed, you can install it using the following commands:
1
2
sudo apt update
sudo apt install libssl-dev
Once you have OpenSSL installed, you can compile and run the code using the following steps:
Save your C code to a file, for example,
elliptic_curve_example.c.Open a terminal and navigate to the directory containing the C file.
Compile the code using the following command:
1
gcc -o elliptic_curve_example elliptic_curve_example.c -lssl -lcrypto
This command tells the compiler to create an executable named elliptic_curve_example from the source code file elliptic_curve_example.c and link it against the OpenSSL library.
- Run the compiled executable:
1
./elliptic_curve_example
This should execute the program, and you should see the output of the key generation, signature creation, and verification process.
Output
1
2
3
4
5
6
┌──(rashid㉿rashid)-[~/Desktop]
└─$ ./elliptic_curve_example
Private Key: C0B710D2E4EF8B3908B8AD6E39EC6A1CFC1978F5784AB7C79C9449BBB3227351
Public Key: 04776B7CF8BC120D3650BCA69D1F81D6391E4107959D4EDB73F7A5671A95D494F3B110C734B9AD9D70070B18D40D365E74DEC5C1EC5D
Signature: 3045022100DD17BB2BE7227D75733B983E7E04FD92EC53041856100E5759FC5C142EABAD4F022003E831AC266AF64DF5A7750A74E537517C5E0EAC0D
Signature verified successfully
Remember that this code uses the secp256k1 curve, which is commonly used in cryptocurrencies like Bitcoin. Ensure that you have the necessary permissions to compile and execute the code in the chosen directory.
Summary In illumos illumos-gate An error occurs in the elliptic curve point addition algorithm that uses mixed Jacobian-affine coordinates where it can yield a result “POINT_AT_INFINITY” when it should not. A man-in-the-middle attacker could use this to interfere with a connection, resulting in an attacked party computing an incorrect shared secret
Description recently i have came across this Tweet from @asanso and thought i should give a try started research on bug which he found in mozilla and ended up finding same bug open source projects this is the blog post for that bug so in this blog post we are going to understand this with some math and elliptic curve, if you love math then you would learn something like i did, but if you are not math lover then you would understand how code base affects and leads to issue which would be helpfull to you in safe coding
Vulnerability Discovery illumos-gate can be found on github.com/illumos here, download it first then we we wanted to do the static-analysis on it open it in any code editor here we gonna use an VSCode, once we opened it vscode all we have to is to look for vulnerable data structure, code lines, statements, to hunt bugs
Steps to reproduce: The implemented elliptic curve point addition algorithm that uses mixed Jacobian-affine coordinates is currently incorrect. It may yield a result POINT_AT_INFINITY when it should not.
Affected Codebase https://github.com/illumos/illumos-gate/blob/master/usr/src/common/crypto/ecc/ecp_jm.c#L126-L136
1
2
3
4
5
6
7
8
9
10
11
/* Computes R = P + Q where R is (rx, ry, rz), P is (px, py, pz) and Q is
* (qx, qy, 1). Elliptic curve points P, Q, and R can all be identical.
* Uses mixed Modified_Jacobian-affine coordinates. Assumes input is
* already field-encoded using field_enc, and returns output that is still
* field-encoded. */
mp_err
ec_GFp_pt_add_jm_aff(const mp_int *px, const mp_int *py, const mp_int *pz,
const mp_int *paz4, const mp_int *qx,
const mp_int *qy, mp_int *rx, mp_int *ry, mp_int *rz,
mp_int *raz4, mp_int scratch[], const ECGroup *group)
{
Original results: The ec_GFp_pt_add_jm_aff implements the algorithm found in “Software Implementation of the NIST Elliptic Curves Over Prime Fields” Here page 12 algorithm 3.
for security reasons github build didnt worked with following pdf but if you google ~francisco/arith/julio.pdf you would find one easily
It does implement the algorithm verbatim as in the paper . The problem is that in the formula reported in the paper is actually incomplete. Indeed it can happen that
C = X2 Z1^2 - A is equal to zero .
[ C = X^2Z^{12} - A ]
This will eventually yield a result POINT_AT_INFINITY (since C is everywhere in the formulas) when it should not.
Expected results: You can find the correct algorithm in https://en.wikibooks.org/wiki/Cryptography/Prime_Curve/Jacobian_Coordinates (Point Addition (12M + 4S)).
lets deeply understand what is Elliptic Curve and Point Addition (12M + 4S) Let (X1, Y1, Z1) and (X2, Y2, Z2) be two points (both unequal to the point at infinity) represented in Jacobian Coordinates. Then the sum (X3, Y3, Z3) can be calculated by
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
U1 = X1*Z2^2
U2 = X2*Z1^2
S1 = Y1*Z2^3
S2 = Y2*Z1^3
if (U1 == U2)
if (S1 != S2)
return POINT_AT_INFINITY
else
return POINT_DOUBLE(X1, Y1, Z1)
H = U2 - U1
R = S2 - S1
X3 = R^2 - H^3 - 2*U1*H^2
Y3 = R*(U1*H^2 - X3) - S1*H^3
Z3 = H*Z1*Z2
return (X3, Y3, Z3)
There this case is taken in consideration
if (U1 == U2) if (S1 != S2) return POINT_AT_INFINITY else return POINT_DOUBLE(X1, Y1, Z1)
and the outcome would be POINT_DOUBLE(X1, Y1, Z1)
Patching this issue was affected to Mozilla Here and mozilla pathed it successfully Patch by them
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
diff --git a/cpputil/scoped_ptrs.h b/cpputil/scoped_ptrs.h
--- a/cpputil/scoped_ptrs.h
+++ b/cpputil/scoped_ptrs.h
@@ -29,16 +29,17 @@ struct ScopedDelete {
void operator()(SECAlgorithmID* id) { SECOID_DestroyAlgorithmID(id, true); }
void operator()(SECItem* item) { SECITEM_FreeItem(item, true); }
void operator()(SECKEYPublicKey* key) { SECKEY_DestroyPublicKey(key); }
void operator()(SECKEYPrivateKey* key) { SECKEY_DestroyPrivateKey(key); }
void operator()(SECKEYPrivateKeyList* list) {
SECKEY_DestroyPrivateKeyList(list);
}
void operator()(PK11URI* uri) { PK11URI_DestroyURI(uri); }
+ void operator()(PLArenaPool* arena) { PORT_FreeArena(arena, PR_FALSE); }
};
template <class T>
struct ScopedMaybeDelete {
void operator()(T* ptr) {
if (ptr) {
ScopedDelete del;
del(ptr);
@@ -57,12 +58,13 @@ SCOPED(PK11SlotInfo);
SCOPED(PK11SymKey);
SCOPED(PRFileDesc);
SCOPED(SECAlgorithmID);
SCOPED(SECItem);
SCOPED(SECKEYPublicKey);
SCOPED(SECKEYPrivateKey);
SCOPED(SECKEYPrivateKeyList);
SCOPED(PK11URI);
+SCOPED(PLArenaPool);
#undef SCOPED
#endif // scoped_ptrs_h__
diff --git a/gtests/freebl_gtest/ecl_unittest.cc b/gtests/freebl_gtest/ecl_unittest.cc
new file mode 100644
--- /dev/null
+++ b/gtests/freebl_gtest/ecl_unittest.cc
@@ -0,0 +1,125 @@
+// This Source Code Form is subject to the terms of the Mozilla Public
+// License, v. 2.0. If a copy of the MPL was not distributed with this file,
+// You can obtain one at http://mozilla.org/MPL/2.0/.
+
+#include "gtest/gtest.h"
+
+#include <stdint.h>
+
+#include "blapi.h"
+#include "scoped_ptrs.h"
+#include "secerr.h"
+
+namespace nss_test {
+
+class ECLTest : public ::testing::Test {
+ protected:
+ const ECCurveName GetCurveName(std::string name) {
+ if (name == "P256") return ECCurve_NIST_P256;
+ if (name == "P384") return ECCurve_NIST_P384;
+ if (name == "P521") return ECCurve_NIST_P521;
+ return ECCurve_pastLastCurve;
+ }
+ std::vector<uint8_t> hexStringToBytes(std::string s) {
+ std::vector<uint8_t> bytes;
+ for (size_t i = 0; i < s.length() - 1; i += 2) {
+ bytes.push_back(std::stoul(s.substr(i, 2), nullptr, 16));
+ }
+ return bytes;
+ }
+ std::string bytesToHexString(std::vector<uint8_t> bytes) {
+ std::stringstream s;
+ for (auto b : bytes) {
+ s << std::setfill('0') << std::setw(2) << std::uppercase << std::hex
+ << static_cast<int>(b);
+ }
+ return s.str();
+ }
+ void ecName2params(const std::string curve, SECItem *params) {
+ SECOidData *oidData = nullptr;
+
+ switch (GetCurveName(curve)) {
+ case ECCurve_NIST_P256:
+ oidData = SECOID_FindOIDByTag(SEC_OID_ANSIX962_EC_PRIME256V1);
+ break;
+ case ECCurve_NIST_P384:
+ oidData = SECOID_FindOIDByTag(SEC_OID_SECG_EC_SECP384R1);
+ break;
+ case ECCurve_NIST_P521:
+ oidData = SECOID_FindOIDByTag(SEC_OID_SECG_EC_SECP521R1);
+ break;
+ default:
+ FAIL();
+ }
+ ASSERT_NE(oidData, nullptr);
+
+ if (SECITEM_AllocItem(NULL, params, (2 + oidData->oid.len)) == NULL) {
+ FAIL() << "Couldn't allocate memory for OID.";
+ }
+ params->data[0] = SEC_ASN1_OBJECT_ID;
+ params->data[1] = oidData->oid.len;
+ memcpy(params->data + 2, oidData->oid.data, oidData->oid.len);
+ }
+
+ void TestECDH_Derive(const std::string p, const std::string secret,
+ const std::string group_name, const std::string result,
+ const bool expect_failure) {
+ ECParams ecParams = {0};
+ ScopedSECItem ecEncodedParams(SECITEM_AllocItem(nullptr, nullptr, 0U));
+ ScopedPLArenaPool arena(PORT_NewArena(DER_DEFAULT_CHUNKSIZE));
+
+ ASSERT_TRUE(arena);
+
+ ecName2params(group_name, ecEncodedParams.get());
+ EC_FillParams(arena.get(), ecEncodedParams.get(), &ecParams);
+
+ std::vector<uint8_t> p_bytes = hexStringToBytes(p);
+ ASSERT_GT(p_bytes.size(), 0U);
+ SECItem public_value = {siBuffer, p_bytes.data(),
+ static_cast<unsigned int>(p_bytes.size())};
+
+ std::vector<uint8_t> secret_bytes = hexStringToBytes(secret);
+ ASSERT_GT(secret_bytes.size(), 0U);
+ SECItem secret_value = {siBuffer, secret_bytes.data(),
+ static_cast<unsigned int>(secret_bytes.size())};
+
+ ScopedSECItem derived_secret(SECITEM_AllocItem(nullptr, nullptr, 0U));
+
+ SECStatus rv = ECDH_Derive(&public_value, &ecParams, &secret_value,
+ PR_FALSE, derived_secret.get());
+ if (expect_failure) {
+ // Abort when we expect an error.
+ ASSERT_EQ(SECFailure, rv);
+ return;
+ } else {
+ ASSERT_EQ(SECSuccess, rv);
+ }
+ std::string derived_result = bytesToHexString(std::vector<uint8_t>(
+ derived_secret->data, derived_secret->data + derived_secret->len));
+ std::cout << "derived secret: " << derived_result << std::endl;
+ EXPECT_EQ(derived_result, result);
+ }
+};
+
+TEST_F(ECLTest, TestECDH_DeriveP256) {
+ TestECDH_Derive(
+ "045ce5c643dffa402bc1837bbcbc223e51d06f20200470d341adfa9deed1bba10e850a16"
+ "368b673732a5c220a778990b22a0e74cdc3b22c7410b9dd552a5635497",
+ "971", "P256", "0", true);
+}
+TEST_F(ECLTest, TestECDH_DeriveP521) {
+ TestECDH_Derive(
+ "04"
+ "00c6858e06b70404e9cd9e3ecb662395b4429c648139053fb521f828af606b4d3dbaa14b"
+ "5e77efe75928fe1dc127a2ffa8de3348b3c1856a429bf97e7e31c2e5bd66"
+ "011839296a789a3bc0045c8a5fb42c7d1bd998f54449579b446817afbd17273e662c97ee"
+ "72995ef42640c550b9013fad0761353c7086a272c24088be94769fd16650",
+ "01fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffa5186"
+ "8783bf2f966b7fcc0148f709a5d03bb5c9b8899c47aebb6fb71e913863f7",
+ "P521",
+ "01BC33425E72A12779EACB2EDCC5B63D1281F7E86DBC7BF99A7ABD0CFE367DE4666D6EDB"
+ "B8525BFFE5222F0702C3096DEC0884CE572F5A15C423FDF44D01DD99C61D",
+ false);
+}
+
+} // nss_test
diff --git a/gtests/freebl_gtest/freebl_gtest.gyp b/gtests/freebl_gtest/freebl_gtest.gyp
--- a/gtests/freebl_gtest/freebl_gtest.gyp
+++ b/gtests/freebl_gtest/freebl_gtest.gyp
@@ -8,16 +8,17 @@
],
'targets': [
{
'target_name': 'freebl_gtest',
'type': 'executable',
'sources': [
'mpi_unittest.cc',
+ 'ecl_unittest.cc',
'<(DEPTH)/gtests/common/gtests.cc'
],
'dependencies': [
'<(DEPTH)/exports.gyp:nss_exports',
'<(DEPTH)/lib/util/util.gyp:nssutil3',
'<(DEPTH)/gtests/google_test/google_test.gyp:gtest',
'<(DEPTH)/lib/nss/nss.gyp:nss_static',
'<(DEPTH)/lib/pk11wrap/pk11wrap.gyp:pk11wrap_static',
@@ -60,16 +61,17 @@
'defines': [
'NSS_USE_STATIC_LIBS'
],
},
],
'target_defaults': {
'include_dirs': [
'<(DEPTH)/lib/freebl/mpi',
+ '<(DEPTH)/lib/freebl/',
],
# For test builds we have to set MPI defines.
'conditions': [
[ 'ct_verif==1', {
'defines': [
'CT_VERIF',
],
}],
diff --git a/gtests/freebl_gtest/mpi_unittest.cc b/gtests/freebl_gtest/mpi_unittest.cc
--- a/gtests/freebl_gtest/mpi_unittest.cc
+++ b/gtests/freebl_gtest/mpi_unittest.cc
@@ -1,21 +1,16 @@
// This Source Code Form is subject to the terms of the Mozilla Public
// License, v. 2.0. If a copy of the MPL was not distributed with this file,
// You can obtain one at http://mozilla.org/MPL/2.0/.
-#include "secdert.h"
-#include "secitem.h"
-#include "secport.h"
-
#include "gtest/gtest.h"
#include <stdint.h>
#include <string.h>
-#include <string>
#ifdef __MACH__
#include <mach/clock.h>
#include <mach/mach.h>
#endif
#include "mpi.h"
namespace nss_test {
diff --git a/lib/freebl/ecl/ecl-priv.h b/lib/freebl/ecl/ecl-priv.h
--- a/lib/freebl/ecl/ecl-priv.h
+++ b/lib/freebl/ecl/ecl-priv.h
@@ -242,9 +242,10 @@ mp_err ec_group_set_gfp521(ECGroup *grou
mp_err ec_group_set_gf2m163(ECGroup *group, ECCurveName name);
mp_err ec_group_set_gf2m193(ECGroup *group, ECCurveName name);
mp_err ec_group_set_gf2m233(ECGroup *group, ECCurveName name);
/* Optimized point multiplication */
mp_err ec_group_set_gfp256_32(ECGroup *group, ECCurveName name);
SECStatus ec_Curve25519_mul(PRUint8 *q, const PRUint8 *s, const PRUint8 *p);
+
#endif /* __ecl_priv_h_ */
diff --git a/lib/freebl/ecl/ecp_jm.c b/lib/freebl/ecl/ecp_jm.c
--- a/lib/freebl/ecl/ecp_jm.c
+++ b/lib/freebl/ecl/ecp_jm.c
@@ -122,16 +122,27 @@ ec_GFp_pt_add_jm_aff(const mp_int *px, c
}
/* A = qx * pz^2, B = qy * pz^3 */
MP_CHECKOK(group->meth->field_sqr(pz, A, group->meth));
MP_CHECKOK(group->meth->field_mul(A, pz, B, group->meth));
MP_CHECKOK(group->meth->field_mul(A, qx, A, group->meth));
MP_CHECKOK(group->meth->field_mul(B, qy, B, group->meth));
+ /* Check P == Q */
+ if (mp_cmp(A, px) == 0) {
+ if (mp_cmp(B, py) == 0) {
+ /* If Px == Qx && Py == Qy, double P. */
+ return ec_GFp_pt_dbl_jm(px, py, pz, paz4, rx, ry, rz, raz4,
+ scratch, group);
+ }
+ /* If Px == Qx && Py != Qy, return point at infinity. */
+ return ec_GFp_pt_set_inf_jac(rx, ry, rz);
+ }
+
/* C = A - px, D = B - py */
MP_CHECKOK(group->meth->field_sub(A, px, C, group->meth));
MP_CHECKOK(group->meth->field_sub(B, py, D, group->meth));
/* C2 = C^2, C3 = C^3 */
MP_CHECKOK(group->meth->field_sqr(C, C2, group->meth));
MP_CHECKOK(group->meth->field_mul(C, C2, C3, group->meth));
Special Thanks I wanted to specially thanks antonio.sanso @asanso , his bug details made me to research more about this bug and as a math lover i digged a lot to understand how it works mathematically and programatically and able to find open source project which is affected by this issue so wants craft a exploit but the issue itself quite challanging and hard by nature but still working on exploit poc
References & Papers https://www.hyperelliptic.org/EFD/oldefd/jacobian.html#:~:text=Jacobian%20coordinates%20represent%20an%20affine,%5E4%20%2B%20bZ%5E6. https://en.wikipedia.org/wiki/Jacobian_curve https://en.wikibooks.org/wiki/Cryptography/Prime_Curve/Jacobian_Coordinates http://delta.cs.cinvestav.mx/~francisco/arith/julio.pdf https://crypto.stackexchange.com/questions/62051/issues-with-elliptic-curve-point-addition https://cve.circl.lu/cve/CVE-2017-7781 https://en.wikipedia.org/wiki/Jacobian_curve https://blog.intothesymmetry.com/2017/08/cve-2017-7781cve-2017-10176-issue-with.html
More Detailed Version Coming Soon